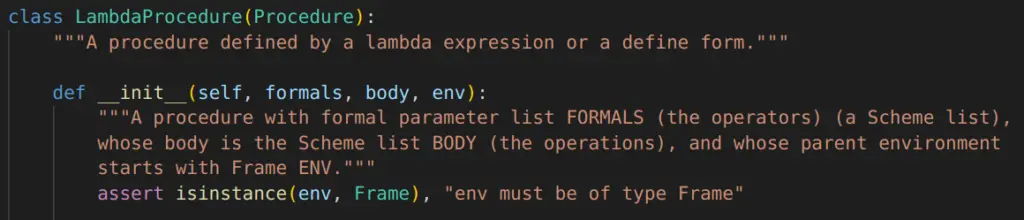
We are finally to the last part of building our interpreter for Scheme in Python. In Part 3 we will implement our special form functions so that we can interpret And/Or, Conditionals, and the Let form in Scheme.
Problem 12: And & Or
Problem 12 deals with the And and Or form. We will be implementing two functions in scheme_forms.py: do_and_form() and do_or_form(). The purpose of these functions are to determine if an expression should evaluate to true or false based off of and/or logic or if it should return a value.
Both functions will intake expressions, which will be a scheme list of individual expressions all represented in Pair objects. Understand that each sub-part of expressions is an expression in scheme being compared to the others by either ‘and‘ or ‘or‘.
Scheme
(and 1 5)
Python
expressions = Pair(1, Pair(5, nil))
In scheme, ‘and‘ by itself evaluates to true, so it is truthy. In contrast, ‘or‘ by itself evaluates to false. We want to make the two functions recursive so that they go through each sub-part of expressions and either returns the value (or true/false if appropriate) or goes on to the next value in the expression.
Check a value’s truthiness using the provided functions: is_scheme_true() and is_scheme_false().
For do_and_form(), if you evaluate any of the expressions and it is a false value, return that value. Else, put the next expression into do_and_form() and recurse on until you get to the end or you get to a false value.
For do_or_form(), if you evaluate any of the expressions and they are truthy, return that value. Else, put the next expression into do_or_form() and recurse on until you get to the end or you get to a true value.
If you go through the entire scheme list of expressions and your function gets to the last element in the scheme list, return the value of that last part.
Hint: What ‘and’ & ‘or’ look like alone
Scheme
(and)
(or)
Python
expressions = nil
expressions = nil
Hint: Evaluating Expressions to Get the Value
Remember to evaluate each scheme expression to get the value of it. We have worked with the function scheme_eval() previously, which is meant to evaluate scheme expressions. We completed it in Problem 6

Problem 13: Cond Form
First of all, lets review the structure of the cond form.
(cond (<predicate 1> <consequent expression>)
(<predicate 2> <consequent expression>)
(<else> <consequent expression>))Each conditional expression will have 1 or more predicates and in many cases will end with an else statement, but not always. We need to implement do_cond_form() such that it takes in expressions and goes through each predicate, testing if it is true. If it is true, it will return the value of the consequent expression. If not it will check the next predicate and do the same thing until we run out of predicates or hit an else statement. If there are no more predicates and no else statement, the function will simply not return anything (None).
The function’s argument expressions will look something like so:
Scheme
(cond ((> 2 3) 5)
(else 8))
Python
expressions = Pair(Pair(Pair(‘>’, Pair(2, Pair(3, nil))), Pair(5, nil)), Pair(Pair(‘else’, Pair(8, nil)), nil))
We are provided some starter code for do_cond_form():
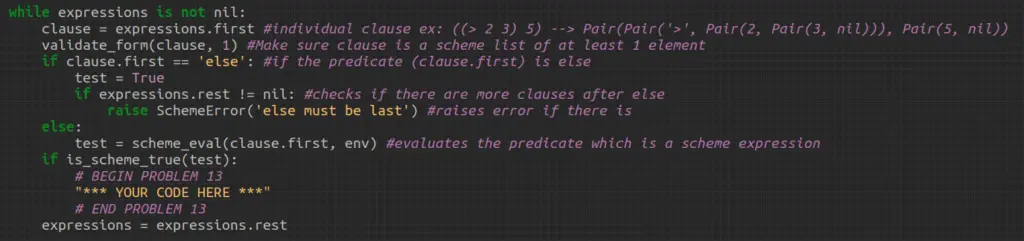
The while loop will run until we hit the end of the list of clauses, meaning expressions.rest will eventually be nil. In the indicated spot, we need to check if the clause has a consequent expression. If it does, we need to evaluate that expression and return it.
Else, check if test is something other than true. If it is something else, that means test (which is an evaluation of the predicate) is just a value like (12), not an expression like (< 1 5) or (else). In that case we simply need to return the evaluation of the predicate.
Lastly, if we get through all of these tests without returning anything, then it could mean two things. Either there was no predicates that were true and there was an else statement, but it did not have a consequent expression. Or it could mean that there was a true predicate without a consequent expression. In these case simply return true.
Problem 14: Let Form
The let form allows us to bind variables locally. This means that when we use let, it creates a new frame in which these variables are defined. Consider the following example from the CS 111 instructions and the added environment diagram.
scm> (define x 5)
x
scm> (define y 'bye)
y
scm> (let ((x 42)
...> (y (* x 10)))
...> (list x y))
(42 50)
scm> (list x y))
(5 bye)Global Frame
x 5
y byeFrame f1
y 50
x 42When the let expression is finished, the frame (f1) is closed and the variables defined by let disappear from the scope of the program. For more information on how let works, consult this page from the University of Texas on the let form. The last three paragraphs are particularly useful. Also refer to the CS 111 specs for let.
To get the let form working in our scheme interpreter, we need to implement the make_let_form() in scheme_forms.py. make_let_frame() will return the new environment with the local variables defined. It takes in two arguments: bindings and env. bindings is a scheme list of variable names and values.
Scheme
scm> (let ((x 5))
…> (+ x 3))
Python
bindings = Pair(Pair(‘x’, Pair(5, nil)), nil)
You are going to need to figure out how you want to iterate through bindings to get each variable name and each value to which it is bound. Hint, you can use a while loop similar to the one in Problem 13.
Check each part of bindings using validate_form() to insure they are the correct format. If the current part of bindings you are checking is the correct format, take the variable name from it and add it to the pre-defined variable names which is a scheme list.
Then use validate_formals() on names to make sure it is still a legitimate format for a scheme list of names.
Next, to get the value, use scheme_eval() to evaluate the part of bindings that is the value. Add that value to the pre-defined variable values which is also a scheme list.
At the end of it all, your function should return a new environment with the new variables and values.
Hint: validate_form()
We want to insure that the bindings put in are correctly formatted. We can check this using validate_form() which takes in three arguments.
validate_form(<list>, <minimum length>, <maximum length>)
There should only be two elements in the bindings we check
Hint: Adding to a Scheme List
scheme_list = nil
scheme_list = Pair(<new_part>, scheme_list)
Hint: Where is the variable name in bindings?
Consider the example:
bindings = Pair(Pair(‘x’, Pair(5, nil)), nil)
The variable name ‘x’ is at bindings.first.first
</end>
Hopefully this was a sufficient help. Please submit any corrections or questions in the comments below. I will try my best to answer and update the article accordingly.